pure_pursuit算法原理

Pure Pursuit是一种几何跟踪控制算法，也被称为纯跟踪控制算法。该算法最早由R. Wallace在1985年提出，其思想是基于当前车辆的后轮中心位置（车辆质心），在参考路径上向$l_d$称为前视距离）的距离匹配一个预瞄点，车辆以一定角度全速向次预瞄点行驶。

假设车辆后轮中心可以按照一定的转弯半径𝑅行驶至该预瞄点，然后根据前视距离$l_d$、转弯半径𝑅、车辆坐标系下预瞄点的朝向角𝛼之间的几何关系来计算前轮转角$\delta$

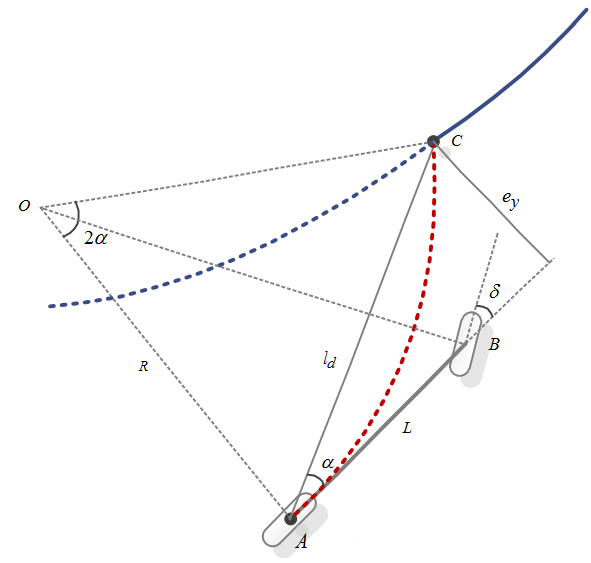
pp算法模型

如上图所示，在三角形OAC中，根据正弦定理可得： $$\frac{l_d}{\sin{\left(2\alpha\right)}}=\frac{R}{\sin{\left(\frac{\pi}{2}-\alpha\right)}}$$

化简得： $$R=\frac{l_d}{2\sin{\left(\alpha\right)}}$$

根据车辆的运动学方程，有： $$\delta=\tan^{-1}{\frac{L}{R}}$$

所以，前轮转角为： $$\delta=\tan^{-1}{\frac{2L\sin{\left(\alpha\right)}}{l_d}}$$

定义横向误差为后轮中心位置和预瞄点在横向上的误差，如上图中的$e_y$ $$e_y=l_d\sin{\left(\alpha\right)}$$

$$sin{\left(\alpha\right)}=\frac{e_y}{l_d}$$

当前轮转角很小是，横向误差可以近似为 $$\delta=\frac{2L}{{l_d}}\sin{\left(\alpha\right)}$$

另外对于非ackerman底盘，尤其是前后轮差距不是很大的底盘(双轮差速加万向轮)，L可以与最大速度v_近似。

$$\delta=\frac{2{v_-}{e_y}}{{l_d}^2}$$

即只要确定了$l_d$，就确定了转向角

基于以上原理，算法步骤为：

1.确定车辆位置和目标点，进行坐标系转换

2.确定转向角$\delta$

3.发布速度指令，全速追踪，更新车辆位置

以下给出非ackerman底盘的pure pursuit算法核心部分具体代码：

    if (!goal_reached_) {
      // We are tracking.
      ROS_INFO("goal_reached_");
      // Compute linear velocity.
      // Right now,this is not very smart :)
      v_ = copysign(v_max_, v_);  // max linear speed

      // Compute the angular velocity.
      // Lateral error is the y-value of the lookahead point (in base_link
      // frame)
      double yt = lookahead_.transform.translation.y;
      double ld_2 = ld_ * ld_;
      // v_可以与L近似，此处为核心代码
      cmd_vel_.angular.z = (-1) * std::min(2 * v_ / ld_2 * yt, w_max_);

      // Set linear velocity for tracking.
      cmd_vel_.linear.x = v_;
      ROS_INFO("here if");
    } else {
      // We are at the goal!

      // Stop the vehicle

      // The lookahead target is at our current pose.
      lookahead_.transform = geometry_msgs::Transform();
      lookahead_.transform.rotation.w = 1.0;

      // Stop moving.
      cmd_vel_.linear.x = 0.0;
      cmd_vel_.angular.z = 0.0;
    }

    // Publish the lookahead target transform.
    lookahead_.header.stamp = ros::Time::now();
    tf_broadcaster_.sendTransform(lookahead_);

    // Publish the velocities
    pub_vel_.publish(cmd_vel_);

参考链接

https://www.mathworks.com/help/robotics/ug/pure-pursuit-controller.html