机器人集群行为仿真与开发
1 什么是集群行为
集群行为的思想最早来源于自然界,主要指一些能力不高的个体在某种形式的配合下,表现出超过个体能力而得以“倍增”的生物现象,如自然界的鸟群、鱼群、蚁群和蜂群等,它能帮助生物躲避天敌、增加寻觅到食物的可能性等。近年来,生物、物理、社会学、计算机和控制领域的学者对自然界的集群行为产生了浓厚的兴趣,并积极从各自领域去探索集群行为产生的原因。
从系统观点看,集群行为具有适应性、鲁棒性、分散性和自组织性,可以从简单的局部规则涌现出协调的全局行为。

图1 自然界的经典集群行为
2 集群行为的数学模型——Boids模型
2.1 Boid是什么
1987年,克雷格•雷诺兹(Craig W. Reynolds)发表了一篇有关集群行为研究的论文,题为《Flocks, herds and schools: A distributed behavioral model》,他提出了一种可以模拟生物集群行为的模型,即Boid模型。Boid是bird-oid object词组的缩写,意为“类似鸟的事物”。在复杂性科学领域中,将克雷格提出的集群行为模型称为“Boids”,集群中的单个个体称为"Boid"。
2.2 Boids模型的基本原则
在自然界,动物集群没有一击而溃的弱点。鸟群迁徙时,即使几只鸟脱离了阵型,鸟群的总体动力学也不会变化。鸟群没有中心节点,没有自上而下的控制,但总体表现出受控的秩序,如图2所示。

图2 自然界的鸟群
克雷格的Boids模型正是以“自下而上的控制”为核心,提出了一个在二维或三维空间上模拟集群行为的模型,该模型要求集群的个体遵守三条基本原则:
- 分离(seperation):与邻域内的集群个体避免碰撞;
- 聚合(cohesion):与邻域内的集群个体保持紧凑;
- 对齐(alignment):与邻域内的集群个体速度保持一致。
将上述三条基本原则衍生的行为按照一定方式加权求和,集群即会出现秩序化的社会性行为,如图3所示。

图3 Boids模型仿真示意图
2.3 分离原则(Seperation)
分离原则是使一个集群个体能够与其附近的集群个体保持一定的间隔距离,从而避免发生碰撞,如图4所示。为了保持彼此分离,一个集群个体首先需要获得邻域内其它集群个体的位置信息。对于一个集群个体来言,每一个在其邻域范围内的集群个体与它之间都有一个排斥力,这个排斥力是与它们之间的距离成反比的。每一个集群个体所受到的排斥力是它邻域范围内其它集群个体对它的排斥力的累加。
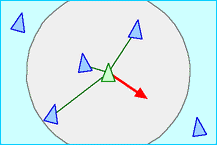
图4 分离原则示意图
按照图论的描述方法,集群内的每个个体 $i$ 都视为图中的一个节点 $V_i$ ,若集群个体 $i$ 可以感知到集群个体 $j$ 的位置和速度信息),则用边 $E_{ij}$ 表示它们存在关联,那么个体 $i$ 的邻近节点集合记为 $N_i={V_j{\in}V:(i,j){\in}E}$ 。分离原则的计算公式如下:
$$\mathbf{u}i^{sep}=\frac{\sum{n=1}^{|N_i|}||\mathbf{q}_i-\mathbf{q}_j||{\cdot}sgn(||\mathbf{q}i-\mathbf{q}j||,d{sep}|)}{\sum{n=1}^{|N_i|}sgn(||\mathbf{q}_i-\mathbf{q}j||,d{sep}|)}$$
$$sgn(x,a)=\left{\begin{array}{lr}1,{\quad}x{\leq}a\0,{\quad}x>a\end{array}\right.$$
其中:
- $\mathbf{u}_i^{sep}$ 为集群个体 $i$ 的分离原则控制量
- $\mathbf{q}_i$ 、 $\mathbf{q}_j$ 为集群个体 $i$ 、 $j$ 的位置
- $d_{sep}$ 为集群个体 $i$ 的排斥距离
- $|N_i|$ 为集群个体 $i$ 邻域内其它集群个体的数量
- $sgn$ 为符号函数。
2.4 聚合原则(cohesion)
聚合原则是使集群具有凝聚力,保持队列的紧凑,如图5 所示。为了能够产生聚合的集群行为,集群个体需要获得其邻域内其它集群个体的位置信息,并计算出邻域内集群个体位置的平均值,由此产生一个作用于该邻域内所有集群个体的吸引力,这样使得集群个体向平均位置方向运动。
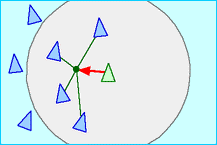
图5 分离原则示意图
聚合原则的计算公式如下:
$$\mathbf{u}i^{coh}=\frac{\sum{n=1}^{|N_i|}\mathbf{q}_j{\cdot}sgn(||\mathbf{q}i-\mathbf{q}j||,d{coh}|)}{\sum{n=1}^{|N_i|}sgn(||\mathbf{q}_i-\mathbf{q}j||,d{coh}|)}-\mathbf{q}_i$$
其中:
- $\mathbf{u}_i^{coh}$ 为集群个体 $i$ 的分离原则控制量
- $d_{coh}$ 为集群个体 $i$ 的聚合距离
- $sgn$ 为符号函数,函数意义同前。
2.5 对齐原则(alignment)
对齐原则使每个集群个体与其邻域内其他集群个体的速度保持一致。如图6 所示。为了能够实现速度一致,每个集群个体需要获得邻域内其它集群个体速度信息,计算出邻域内集群个体的平均速度。通过速度对齐,可以使得集群个体速度大小和方向与这个邻域内所有集群个体速度的平均值保持一致。
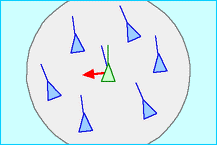
图6 对齐原则示意图
对齐原则的计算公式如下:
$$\mathbf{u}i^{ali}=\frac{\sum{n=1}^{|N_i|}\mathbf{p}_j{\cdot}sgn(||\mathbf{q}i-\mathbf{q}j||,d{ali}|)}{\sum{n=1}^{|N_i|}sgn(||\mathbf{q}_i-\mathbf{q}j||,d{ali}|)}$$
其中:
- $\mathbf{u}_i^{ali}$ 为集群个体 $i$ 的分离原则控制量
- $\mathbf{q}_j$ 为集群个体 $i$ 的速度
- $sgn$ 为符号函数,函数意义同前。
2.6 Boids数学模型
由于雷诺兹所提出的三条基本原则实际上是基于系统环境中集群个体的位置和速度来考虑的。假设有 $N$ 个集群个体在 $n$ 维的欧式空间中运行,则第 $i$ 个集群个体的二阶运动方程为:
$$\begin{array}{lr}\mathbf{\dot{q}}_i=\mathbf{p}_i\\mathbf{\dot{p}}_i=\mathbf{u}_i,i=1,...,N\end{array}$$
其中:
- $\mathbf{q}_i\in{\mathbf{R}^n}$ 代表集群个体 $i$ 的位置向量
- $\mathbf{p}_i\in{\mathbf{R}^n}$ 代表集群个体 $i$ 的速度矢量
- $\mathbf{u}_i\in{\mathbf{R}^n}$ 代表集群个体 $i$ 的控制输入(加速度)向量
根据雷诺兹所提出的三条基本原则,将 $\mathbf{u}_i^{sep}$ 、 $\mathbf{u}_i^{coh}$ 、 $\mathbf{u}_i^{ali}$ 三个控制量加权求和,输入到集群系统中即可实现集群行为,其控制量的计算公式如下:
$$ \mathbf{u}i=\omega{sep}\cdot\mathbf{u}i^{sep}+\omega{coh}\cdot\mathbf{u}i^{coh}+\omega{ali}\cdot\mathbf{u}_i^{ali} $$
其中: $\omega_{sep}$ 、 $\omega_{coh}$ 、 $\omega_{ali}$ 分别表示 $\mathbf{u}i^{sep}$ 、 $\mathbf{u}i^{coh}$ 、 $\mathbf{u}i^{ali}$ 控制量的权重,且 $\omega{sep},\omega{coh},\omega{ali}\geq0$ 。
3 Boids数学模型的改进
由于雷诺兹所提出的Boids数学模型初始条件(如初始位置和速度)任意选取的,可能会产生分裂现象。如图7所示,整个集群会被分成三个子集群,每个子集群的个体只能与其所在子集群内的个体交互,由此产生了分裂现象。在实际的机器人集群控制应用中,集群需要在有限空间(二维或三维)上运动,则要考虑边界避碰和障碍物避碰的情况。同时,整个机器人集群并不是漫无目的地机动,需要对其机动方向和速度加以引导。为此,我们在Boids数学模型的基础上,增加了边界避碰、障碍物避碰和领导者-跟随者三条原则。
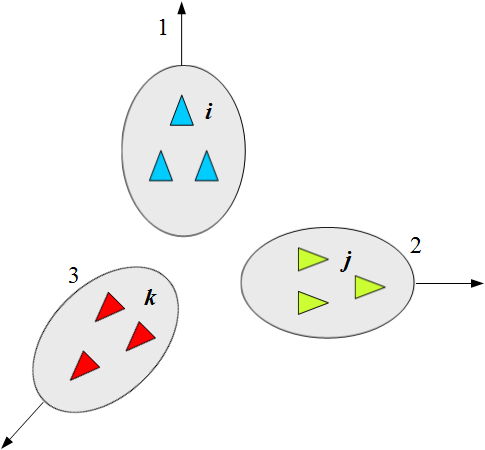
图7 分裂现象
3.1 触界反弹原则
触界反弹原则是每个集群个体与人为设置的虚拟边界保持一定的间隔距离,从而避免发生碰撞,如图8所示。当某个集群个体与虚拟边界的距离小于某个阈值 $d_{border}$ 时,会产生一个触界反弹的排斥力。
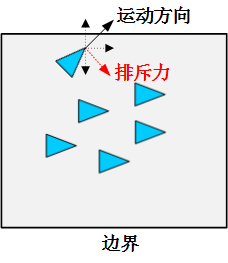
图8 边界避碰原则示意图
边界避碰原则的计算公式如下: $$ \mathbf{u_i^{border}}=k_1\cdot\mathbf{p}{border}\cdot{sgn(d{i,border},d_{border})} $$ 其中:
- $\mathbf{p}_{border}$ 表示集群个体在虚拟边界所产生的排斥力
- $d_{i,border}$ 表示集群个体 $i$ 与虚拟边界的距离
- $k_1$ 表示调节系数,且 $k_1<0$
- $sgn$ 为符号函数,函数意义同前。
3.2 障碍物避碰原则
障碍物避碰原则是每个集群个体与障碍物保持一定的间隔距离,从而避免发生碰撞,如图9所示。当某个集群个体与障碍物的距离小于某个阈值 $d_{obs}$ 时,会产生一个排斥力,这个排斥力是与它们之间的距离成反比。
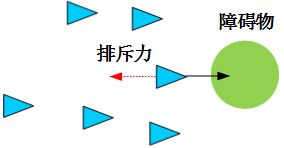
图9 障碍物避碰原则示意图
障碍物避碰原则的计算公式如下: $$ \mathbf{u}i^{obs}=k_2\cdot\sum{l=1}^{L}||\mathbf{q}_i-\mathbf{q}_l^{obs}||{\cdot}sgn(||\mathbf{q}_i-\mathbf{q}l^{obs}||,d{obs}) $$ 其中:
- $\mathbf{u}_i^{obs}$ 为集群个体 $i$ 的障碍物避碰原则控制量
- $\mathbf{q}_l^{obs}$ 为第 $l$ 个障碍物的位置
- $k_2$ 表示调节系数,且 $k_2<0$
- $sgn$为符号函数,函数意义同前。
3.3 领导者-跟随者原则
领导者-跟随者原则是在集群运动中加入引导信息,引导集群以期望的速度向某个目的地运动。根据该原则,可在集群内设置虚拟领导者或真实领导者(即指定某个集群个体为领导者,其它集群个体为跟随者)。引导信息分为两个部分,一是领导者的期望速度 $\mathbf{p}{leader}$ ,二是领导者的目的地位置 $\mathbf{q}{leader}$ ,其计算公式如下: $$ \mathbf{u}i^{leader}=c_1(\mathbf{q}{leader}-\mathbf{q}i)+c_2(\mathbf{p}{leader}-\mathbf{p}_i) $$ 其中:
- $\mathbf{u}_i^{leader}$ 为集群个体 $i$ 的领导者-跟随者原则控制量
- $c_1$ 、 $c_2$ 为调节系数,且 $c_1>0,c_2>0$
3.4 改进型Boids数学模型
在雷诺兹所提出的Boids数学模型基础上,综合边界避碰、障碍物避碰和领导者-跟随者三条原则,可以得到改进型的Boids数学模型,其控制量的计算公式如下: $$ \mathbf{u}i=\omega{sep}\cdot\mathbf{u}i^{sep}+\omega{coh}\cdot\mathbf{u}i^{coh}+\omega{ali}\cdot\mathbf{u}i^{ali}+\omega{border}\cdot\mathbf{u}i^{border}+\omega{obs}\cdot\mathbf{u}i^{obs}+\omega{leader}\cdot\mathbf{u}_i^{leader} $$ 其中:
- $\omega_{border}$ 、 $\omega_{obs}$ 、 $\omega_{leader}$ 分别表示 $\mathbf{u}i^{border}$ 、 $\mathbf{u}i^{obs}$ 、 $\mathbf{u}i^{leader}$ 控制量的权重,且 $\omega{border},\omega{obs},\omega{leader}\geq0$ , $\omega_{sep}$ 、 $\omega_{coh}$ 、 $\omega_{ali}$ 符号意义同前。
4 机器人集群行为开发
机器人集群的设计灵感来源于自然界的自组织系统,例如社交昆虫、鱼类或鸟群,它们都是基于简单本地交互规则的涌现性群体行为。为此,我们基于雷诺兹所提出的的Boids数学模型,构建比单个机器人更加鲁棒、更强容错和更高灵活的系统,并且能够更好地调整自身行为来适应环境变化。
4.1 集群行为仿真开发流程
我们将机器人集群抽象为复杂系统,每个集群机器人都是复杂系统的智能个体,智能个体不仅能感知物理环境,还能感知同伴的活动,最后根据这些信息决定如何移动。在仿真建模过程中,可以利用形式最为简单的粒子系统进行模拟。一般情况下,用简单的图形或者点表示粒子,每个粒子的移动方式遵循牛顿第二定律,粒子之间可以进行简单的信息交互(如接收同伴的位置和速度信息),但交互能力有限制,不能与所有同伴进行交互。
具体的仿真开发流程如图10所示,智能个体主要由信息交互、控制和机动三大核心模块构成,信息交互模块主要获取其它智能个体的位置和速度信息,并将该信息传递给控制模块,控制模块主要根据集群控制算法计算得到智能个体关于线速度和角速度的控制量,并将控制量信息传递给机动模块,智能个体按照牛顿第二定律进行移动,输出关于位置和速度的运动状态信息,并将该信息传递给其它智能个体的信息交互模块。
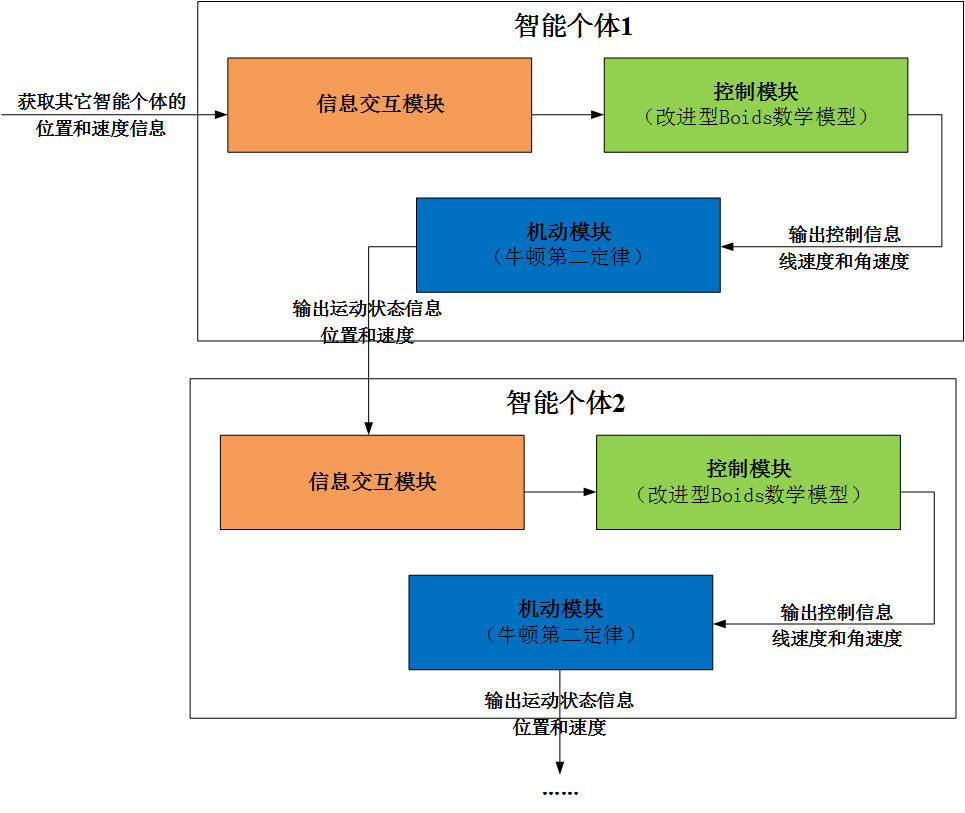
图10 仿真开发流程示意图
4.2 集群行为控制示例代码
集群控制函数主要实现改进型Boids数学模型的功能,根据自身和其它智能个体的运动状态信息计算其在下一个仿真步长的运动控制量。
4.2.1 分离原则
示例代码如下:
function steer = separate(boid_id, boids_num, flock_pos, sep_dist, boid_maxspeed)
steer = [0.0, 0.0];
count = 0;
this_boid_loc = flock_pos(:,boid_id);
for i=1:boids_num
if boid_id==i
continue;
end
other_boid_loc = flock_pos(:,i);
d = vec_dist(this_boid_loc', other_boid_loc');
if d>0 && d < sep_dist
diff = this_boid_loc'- other_boid_loc';
diff = vec_normalize(diff);
diff = diff*(1.0/d);
steer = steer + diff;
count = count + 1;
end
end
if count>0
steer = steer * (1.0/count);
end
if vec_mag(steer)>0
steer = vec_normalize(steer);
steer = steer * boid_maxspeed;
end
end
4.3 聚合原则
示例代码如下:
function steer = cohesion(boid_id, boids_num, flock_pos, coh_dist, boid_maxspeed)
steer = [0.0, 0.0];
count = 0;
this_boid_loc = flock_pos(:,boid_id);
for i=1:boids_num
if boid_id==i
continue;
end
other_boid_loc = flock_pos(:,i);
d = vec_dist(this_boid_loc', other_boid_loc');
if d>0 && d < coh_dist
steer = steer + other_boid_loc';
count = count + 1;
end
end
if count>0
steer = steer * (1.0/count);
steer = seek(steer, this_boid_loc', boid_maxspeed);
end
end
4.4 对齐原则
示例代码如下:
function steer = align(boid_id, boids_num, flock_pos, flock_vel, coh_dist, boid_maxspeed)
steer = [0.0, 0.0];
count = 0;
this_boid_loc = flock_pos(:,boid_id);
for i=1:boids_num
if boid_id==i
continue;
end
other_boid_loc = flock_pos(:,i);
d = vec_dist(this_boid_loc', other_boid_loc');
if d>0 && d < coh_dist
steer = steer + flock_vel(:,i)';
count = count + 1;
end
end
if count>0
steer = steer*(1.0/count);
steer = vec_normalize(steer);
steer = steer * boid_maxspeed;
end
end
4.5 触界反弹原则
示例代码如下:
function [steer, current_this_boid_flag,flock_avoid_vel] = border_fear(boid_id, second_paras, x,y , vx,vy, flock_avoid_vel, flock_border_flag, avoid_border_dist, boid_maxspeed)
x_low = second_paras(1) + avoid_border_dist;
x_high = second_paras(2) - avoid_border_dist;
y_low = second_paras(3) + avoid_border_dist;
y_high = second_paras(4) - avoid_border_dist;
current_this_boid_flag = is_in_border(x, y, x_low, x_high, y_low, y_high);
if current_this_boid_flag == 0
steer = [0.0, 0.0];
else
old_this_boid_flag = flock_border_flag(boid_id);
this_boid_avoid_vel = flock_avoid_vel(:, boid_id)';
if old_this_boid_flag>0 && current_this_boid_flag>0 && old_this_boid_flag~=current_this_boid_flag
this_boid_avoid_vel = [0.0, 0.0];
% 鍙宠竟鐣?
if x >= x_high
if vx>=0
vx = -vx;
end
end
% 宸﹁竟鐣?
if x <= x_low
if vx < 0
vx = -vx;
end
end
% 涓婅竟鐣?
if y >= y_high
if vy >=0
vy = -vy;
end
end
% 涓嬭竟鐣?
if y <= y_low
if vy < 0
vy = -vy;
end
end
this_boid_avoid_vel = [vx, vy];
flock_avoid_vel(1, boid_id) = vx;
flock_avoid_vel(2, boid_id) = vy;
end
steer = this_boid_avoid_vel;
if vec_mag(steer)>0
steer = vec_normalize(steer);
steer = steer * boid_maxspeed;
else
steer = [0.0, 0.0];
end
end
end
4.6 避障原则
示例代码如下:
function desired = obstacle_fear(boid_id, flock_pos, obstacle_num, ob_pos, avoid_obs_dist, boid_maxspeed)
steer = [0.0, 0.0];
desired = [0.0, 0.0];
count = 0;
this_boid_loc = flock_pos(:,boid_id)';
for i=1:obstacle_num
this_ob_loc = ob_pos(:,i)';
steer = this_boid_loc - this_ob_loc;
if vec_mag(steer) <= (0.15 + avoid_obs_dist)
desired = desired + steer
count = count + 1;
end
end
if count > 0
desired = vec_normalize(desired);
desired = desired * boid_maxspeed;
end
end
4.7 领导者-跟随者原则
示例代码如下:
function [steer,new_waypt_id] = virtual_leader(boid_id, wp_ids, flock_pos, waypoint_num, waypoints, boid_maxspeed)
steer = [0.0, 0.0];
this_boid_loc = flock_pos(:, boid_id)';
new_waypt_id = set_waypoint(boid_id, wp_ids, flock_pos, waypoint_num, waypoints);
curr_waypt = waypoints(:,new_waypt_id)';
steer = curr_waypt - this_boid_loc;
if vec_mag(steer) > 0
steer = vec_normalize(steer);
steer = steer * boid_maxspeed;
end
end
参考文献
[1]Flocks, herds and schools: A distributed behavioral model
[2]Daniel Shiffman. 代码本色$\cdot$用编程模拟自然系统[M].人民邮电出版社,2021:218-269.
[3]苏厚胜
[4]Swarm Robotics: Past, Present, and Future