基于深度强化学习的跟车策略学习方法
一、强化学习基本原理
1.1 什么是强化学习
强化学习旨在学习如何做,即如何根据情况采取动作,从而实现数值奖励信号最大化。学习者不会接到动作指令,而是必须自行尝试发现回报最高的动作方案。
—Sutton and Barto,强化学习导论
1.2 强化学习与传统控制的关系
强化学习 (RL) 已成功地训练计算机程序在游戏中击败全球最厉害的人类玩家。在状态和动作空间较大、环境信息不完善并且短期动作的长期回报不确定的游戏中,这些程序可以找出最佳动作。
图1-1 人机大战
在为真实系统设计控制器的过程中,工程师面临同样的挑战,如控制机器人走路或自动驾驶汽车。

图1-2 机器人走路

图1-3 自动驾驶
1.2.1 控制目标
从广义上而言,控制系统的目标是确定正确的系统输入(动作),从而生成期望的系统行为。在反馈控制系统中,控制器使用状态观测提高性能并修正随机干扰。工程师描述被控对象和环境模型,运用反馈信号,设计控制器,从而满足系统需求。以上概念表述十分简单;然而,倘若系统难以建模、高度非线性或者状态和动作空间较大,则很难实现控制目标。
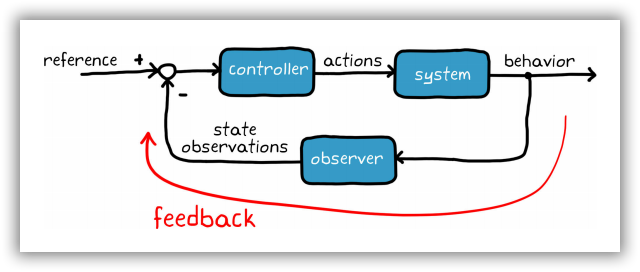
图1-4 传统的控制器设计示意图
1.2.2 控制问题
为了理解此类难题对控制设计问题造成的进一步后果,不妨设想一下开发步行机器人控制系统的场景。要控制机器人(即系统),可能需要命令数十台电机操控四肢的各个关节。每一项命令是一个可执行的动作。系统状态观测量有多种来源,包括摄像机视觉传感器、加速度计、陀螺仪及各电机的编码器。
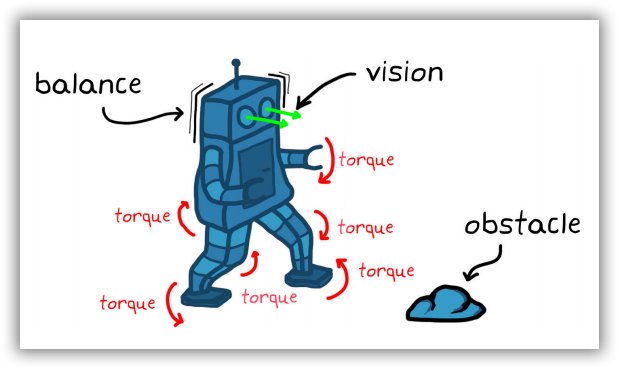
图1-5 行走机器人的控制问题
控制器必须满足多项要求:
• 确定适当的电机扭矩组合,确保机器人正常步行并保持躯体平衡。
• 需要在避开多种随机障碍物的环境下操作。
• 抗干扰,如阵风。
控制系统设计不仅要满足上述要求,还需满足其他附加条件,比如在陡峭的山坡或冰块上行走时保持平衡。
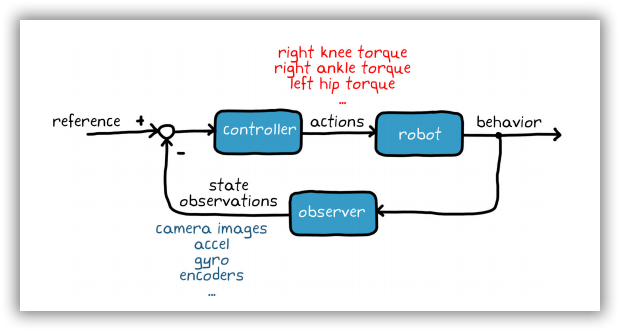
图1-6 行走机器人控制器需要考虑的问题
1.2.3 传统的控制方案
通常,解决此类问题的最佳方法是将问题分解成为若干部分,逐个击破。
如图1-7所示,我们可以构建一个提取摄像机图像特征的流程。例如,障碍物的位置和类型,或者机器人在全局参照系中所处的位置。综合运用这些状态与其他传感器传回的处理后的观测值,完成全状态估测。 估算的状态值和参考值将反馈给控制器,其中很可能包含多个嵌套控制回路。外部环路负责管理高级机器人行为(如保持平衡),内部环路用于管理低级行为和各个作动器。
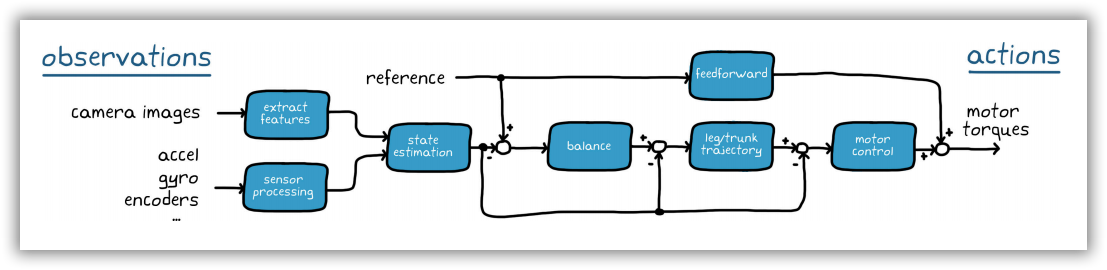
图1-7 行走机器人的控制器设计方案
这种控制方案要求各环路之间相互交互,使得设计和调优变得异常困难。同时,确定最佳的环路构造和问题分解也并不轻松。
1.2.4 强化学习的控制方案
如果不是尝试单独设计每一个组件,而是设想一下将其全部塞进一个函数里, 由该函数负责接收所有观察结果并直接输出低级动作。 毋庸置疑,这可以简化系统方块图,但这个函数会是怎样的结构?我们该如何设计这个函数呢?创建一个单一的大函数比构建由分段子组件构成的控制系统,看起来难度要大;不过,强化学习可以帮助我们达成目标。
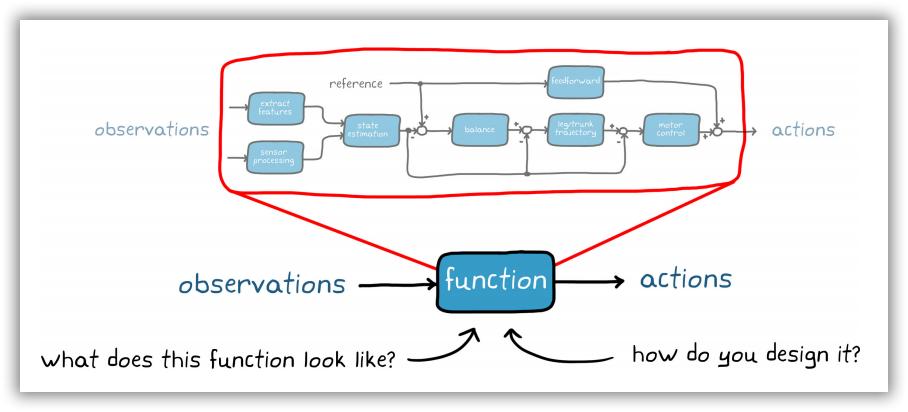
图1-8 基于强化学习的行走机器人控制器设计方案
1.3 强化学习的基本原理与流程
1.3.1 强化学习的基本原理
与传统监督学习与无监督学习不同,强化学习采用动态环境数据,其目标并不是对数据进行分类或标注,而是确定生成最优结果的最佳动作序列,通过一个所谓的智能体(agent)来探索环境、与环境交互并从环境中学习。
智能体中有一个函数可接收状态观测量(输入),并将其映射到动作集(输出)。也就是前面提到过的单一函数,它将取代控制系统的所有独立子组件。在RL 命名法中,此函数称之为策略。策略根据一组给定的观测量决定要采取的动作。
以步行机器人为例,观察结果是指每个关节的角度、机器人躯干的加速度和角速度,以及视觉传感器采集的成千上万个像素点。策略将根据所有这些观测量,输出电机指令,使机器人移动四肢。随后,环境将生成奖励,向代理反映特定作动器指令组合的效果。如果机器人能够保持直立并继续行走,对应的奖励则将高于机器人摔倒时的奖励。
如果可以设计出一项完美的策略,针对观察到的每一种状态向适当的作动器发出适当的指令,那么目标就达成了。因此,强化学习算法应运而生。它可以根据已采取的动作、环境状态观测量以及获得的奖励值来改变策略。智能体的目标是使用强化学习算法学习最佳环境交互策略;这样一来,无论在任何状态下,智能体都能始终采取最优动作——即长期奖励最丰厚的动作。
强化学习的目标与控制问题相似,只不过方法不同,使用不同的术语表示相同的概念。 通过这两种方法,我们希望确定正确的系统输入,从而让系统产生期望的行为。 我们的目的在于判断如何设计策略(或控制器),从而将环境(或被控对象)的状态观测量映射到最佳动作(作动器指令)。 状态反馈信号是指环境观察结果,参考信号则内置到奖励函数和环境观测量中。
1.3.2 强化学习的基本流程
如图1-9所示,强化学习一般涉及到五个步骤,分别是建立环境,设计奖励信号,研究策略表示方法、设计训练算法,验证部署。其中,我们需要一个环境,供智能体开展学习,需要选择环境里应该有什么,是虚拟的仿真环境还是真实的物理环境; 需要考虑最终想要智能体做什么工作,并设计奖励函数, 激励智能体实现目标;需要选择一种表示策略的方法,思考如何构造参数和逻辑,由此构成智能体的决策部分;需要选择一种算法来训练智能体,争取找到最优的策略参数;需要在实地部署该策略并验证结果, 从而利用该策略。
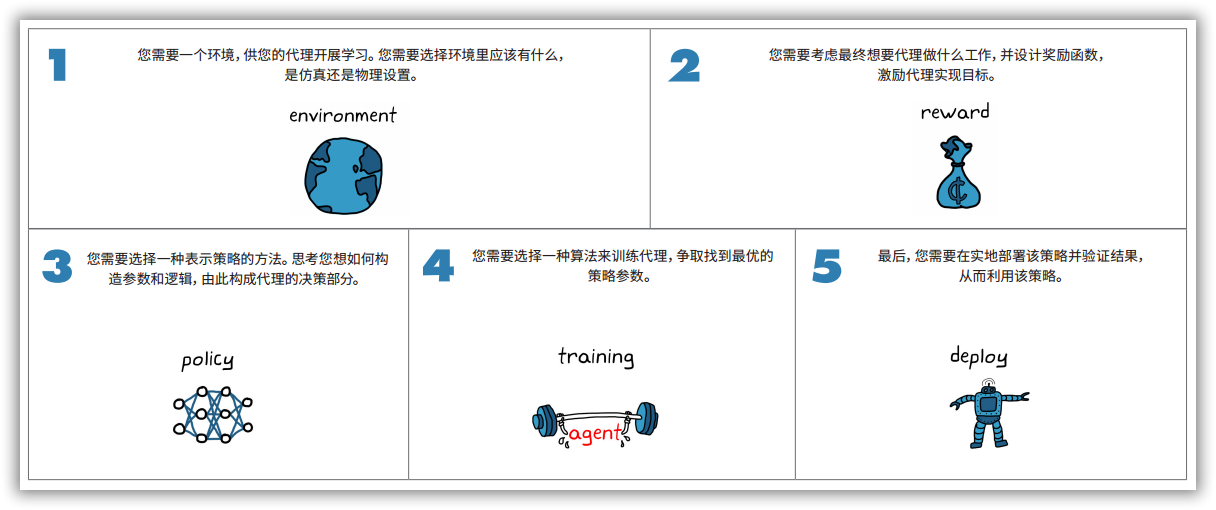
图1-9 强化学习的基本流程
二、跟车问题描述
跟车问题是指通过控制车辆自身的转向角度和速度,与领头车保持一定的安全距离,跟随领头车行驶。跟车问题在学术领域被称为路径跟随问题,目前该问题有很多解决方法,如模型预测控制方法,感兴趣的朋友可以参考软件Matlab提供的路径跟随控制系统。在这里,我们采用当前人工智能最为流行的深度强化学习方法来解决该问题。
2.1 马尔科夫决策过程
针对路径跟随问题,可以采用马尔科夫决策过程进行描述,即用四元组$E=<S,A,P,R>$,$E$为当前的路径跟随环境,$S$为路径跟随小车观测外部环境的状态空间,$A$为路径跟随小车的动作空间,$P$为状态转移函数,$R$为奖励函数。在某一时刻$t$,路径跟随小车agent观测外部环境的状态记为$s_t$,根据所学习的跟车策略$\pi(s_t)$输出动作$a_t$,并从外部环境获取即时奖励$r_t=R(s_t,a_t)$。
如图2-1所示,给出了路径跟随示意图。其中,领头车为蓝色小车,跟随车为黄色小车,$e_1$、$e_2$为领头车与跟随车的横向偏移距离和纵向偏移距离,$d_{rel}$为领头车与跟随车的偏移距离,$\theta_{yaw1}$、$\theta_{yaw2}$为领头车和跟随车的绝对航向角(与$x$轴的夹角,按逆时针旋转为正方向)。跟随车需要与领头车保持一定的纵向偏移距离和速度,同时横向偏移距离不能过大,才能保证较好的路径跟随效果。

图2-1 路径跟随示意图
2.2 状态空间设计
在状态空间设计中,我们认为领头车与跟随车的相对位置$(\Delta{x},\Delta{y})$、相对航向角$\Delta{\theta}$、横向偏移距离$e_1$、纵向偏移距离$e_2$、跟随车的线速度$V_{ego}$以及参考速度$V_{ref}$与线速度之差$e_V$、横向偏移距离变化率$\dot{e}1$和相对航向角变化率${\Delta}\dot{\theta}$,这些因素都会对路径跟随效果有一定影响。其中,跟随车的参考速度$V{ref}$主要根据领头车的线速度$V_{lead}$、预设的跟随车线速度$V_{set}$以及领头车与跟随车的安全距离$d_{safe}$进行计算,而将安全距离$d_{safe}$定义成与跟随车线速度有关的线性函数,即$d_{safe}=t_{gap}*V_{ego}+d_{default}$,$t_{gap}$、$d_{default}$分别为常量。当$d_{safe}-d_{rel}>0$时,取领头车线速度和跟随车预设线速度的最小值,反之,取随车预设得线速度,故跟随车的参考速度$V_{ref}$可以看成是领头车与跟随车的安全距离$d_{safe}$的映射函数。 $$ V_{ref}=\left{\begin{array}{}min(V_{lead},V_{set}) & d_{safe}-d_{rel}>0\V_{set}, & d_{safe}-d_{rel}{\leq}0\end{array}\right. $$
由此,跟随车的状态空间可采用九元组进行表示,即$<\Delta{x},\Delta{y},\Delta{\theta},V_{ego},e_V,e_1,e_2,\dot{e}_1,{\Delta}\dot{\theta}>$
2.3 奖励函数设计
在强化学习算法中,奖励函数设计是极其重要的一环,它可以将任务目标具体化、数值化,奖励函数设计的好坏直接体现了其对任务逻辑的理解深度,决定了智能体最终能否学到期望的行为策略,从而影响算法的收敛速度和最终性能。
为了保证较好的路径跟随效果,需要对以下几个方面进行考虑:
- 跟随车的参考速度$V_{ref}$与线速度$V_ego$之差$e_v$不能太大;
- 领头车与跟随车的横向漂移距离$e_1$不能太大;
- 跟随车上一次角速度$w_{t-1}$和线速度$v_{t-1}$控制量幅度不能太大;
- 领头车与跟随车的横向和纵向漂移距离较大时,将受到惩罚。
根据上述情况,路径跟随的奖励函数设计为:
$r_t=-0.1e_v^2-0.1e_1^2-0.1\omega_{t-1}^2-0.5v_{t-1}-10F_t+M_t+2H_t$
其中,$e_v$为前车与后车的纵向速度差(m/s),$e_v=V_{ref}-V_{ego}$;当领头车与跟随车的横向和纵向漂移距离较大时,$F_t=1$,否则,$F_t=0$;当$e_v^2<1$时,$M_t=1$,否则,$M_t=0$;当$e_1^2<0.01$时,$H_t=1$,否则,$H_t=0$;
2.4 动作空间设计
在路径跟随环境中,车辆采用的是双轮差速模型,其控制变量主要有线速度和角速度。为保证车辆控制的平滑性和稳定性,将线速度和角速度按照连续动作进行设计。
三、跟车仿真环境搭建
详见 仿真系统搭建
3.2 基于Simulink的跟车仿真环境
3.2.1 车辆模型
在路径跟随环境中,领头车和跟随车的运动模型将采用Matlab提供的双轮差速模型,该模型主要模拟位置矢量$q=[x,y,\theta]^T$、运动速度矢量$u=[v,w]^T$($w$为瞬时角速度、$v$为瞬时线速度),两个矢量的关系如下式所示。 $$ \dot{q}=S\cdot{u} $$ 其中,$S=\left[ \begin{array}{l} cos\theta & 0 \ sin\theta & 0 \ 0 & 1 \end{array} \right]$。该模型的输入为运动速度矢量(线速度与角速度),输出为位置矢量,可以根据速度的变化得到小车模型下一时刻的位置。
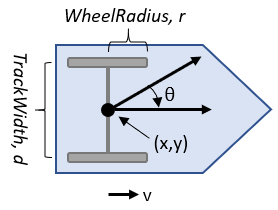
图3-23 双轮差速模型
关于车辆模型,Matlab提供了基本参数:
- 车轮半径wheel radius:车轮的半径将影响运动时的速度与位置关系,默认为0.05;
- 车轮速度范围wheel speed range:线速度和角速度的范围,默认为负无穷到正无穷;
- 轮距track width:两轮之间的距离,默认为0.2;
- 控制方式vehicle inputs:matlab提供了两种,一是Wheel Speeds,即输入左右轮的速度;二是Vehicle Speed Heading Rate,即输入线速度和角速度。
3.2.2 领头车机动控制模型
Matlab除了提供3.2.1节所述的双轮差速模型,还提供了controller Pure Pursuit控制器,该控制器能够实现车辆按照预设的航路点运动。如图3-24所示,根据路径跟随环境的需要,在指定区域设置四个航路点,领头车将沿着四个航路点循环往复运动,跟随车将按照领头车的运动轨迹跟随。
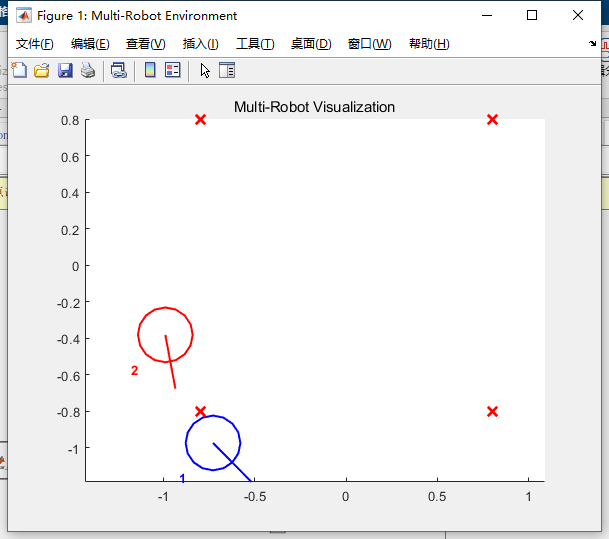
图3-24 领头车的四个航路点
3.2.3 跟车的状态输入、奖励计算与动作输出
3.2.3.1 状态输入
根据3.2节的状态空间设计,提供强化学习算法所需要的状态输入,示例代码如下:
function observation = get_obs(x1,x2,y1,y2,lateral_rel_dist, longitudinal_rel_dist,
yaw1, yaw2, leader_linear_vel, ego_linear_vel, ...
yaw_delta_former, lateral_rel_dist_former)
% 状态空间
% 输入
% longitudinal_rel_dist 领头车与跟随车的纵向相对距离
% lateral_rel_dist 领头车与跟随车的横向相对距离
% yaw_delta 领头车与跟随车的航向角偏差
% ego_linear_vel 跟随车的线速度
% e_v 跟随车的参考速度与线速度之差
% lateral_rel_dist_dot 领头车与跟随车的横向相对距离变化率
% yaw_delta_dot 领头车与跟随车的航向角偏差变化率
% 计算领头车与跟随车的相对位置
x_delta = x1 - x2;
y_delta = y1 - y2;
% 计算领头车与跟随车的绝对航向角之差
yaw_delta = yaw1-yaw2;
% 计算跟随车的横向偏移距离变化率和相对航向角变化率
lateral_rel_dist_dot = lateral_rel_dist - lateral_rel_dist_former;
yaw_delta_dot = yaw_delta - yaw_delta_former;
% 计算跟随车的参考速度与线速度之差
v_ref = get_ref_velocity(leader_linear_vel, ...
ego_linear_vel, longitudinal_rel_dist);
e_v = v_ref - ego_linear_vel;
observation = [x_delta, y_delta, longitudinal_rel_dist,e_v, ego_linear_vel, ...
lateral_rel_dist, lateral_rel_dist_dot, yaw_delta, yaw_delta_dot];
end
3.2.3.2 奖励计算
根据3.3节的奖励函数设计,计算跟随车在跟随过程中的即时奖励,示例代码如下:
function reward = reward_calc(e_v, lateral_rel_dist, ego_linear_vel,... ego_omega_vel, last_ego_omega_vel, isDone)
% e_v 跟随车参考速度与线速度之差
% lateral_rel_dist 领头车与跟随车的横向相对距离
% ego_linear_vel 跟随车的线速度
% ego_omega_vel 跟随车的角速度
% last_ego_omega_vel 跟随车上一次的角速度
% isDone 判断仿真是否终止 0表示仿真继续 1表示仿真终止
F_t = 0.0;
M_t = 0.0;
H_t = 0.0;
delta_omega = 0.0;
e_v_square = e_v * e_v;
lateral_rel_dist_square = lateral_rel_dist * lateral_rel_dist;
if isDone==1
F_t = 1.0;
end
if e_v_square < 1.0
M_t = 1.0;
end
if lateral_rel_dist_square<0.01
H_t = 1.0;
end
if sim_step >= 2
delta_omega = ego_omega_vel - last_ego_omega_vel;
end
reward = -0.1*e_v_square - 0.1*ego_linear_vel*ego_linear_vel- ... 0.1*lateral_rel_dist_square - 0.5*ego_omega_vel*ego_omega_vel -...
0.4*delta_omega*delta_omega - 10.0*F_t + M_t + + 2.0*H_t;
end
3.2.3.3 动作输出
在路径跟随环境中,跟随车的线速度控制在0.15-0.25m/s范围内,角速度控制在-1.0~1.0rad/s范围内,强化学习算法采用连续类型的控制量控制跟随车运动。如图所示,给出了跟随车的线速度和角速度的限幅范围。
3.2.4 仿真环境终止条件
当出现以下三种情况时,仿真将终止:
-
跟随车与领头车发生碰撞
-
跟随车与领头车的横向偏移距离超出阈值
-
跟随车与领头车的纵向偏移距离超出阈值
其示例代码如下:
function flag = EnvisDone(rel_dist, lateral_rel_dist, longitudinal_rel_dist, ego_linear_vel)
% avoid_dist 领头车与跟随车的碰撞距离
% max_lateral_rel_dist 跟车的横向最大偏移距离
% max_longitudinal_rel_dist 跟车的纵向最大偏移距离
flag = 0;
avoid_dist = 0.3;
min_ego_linear_vel = 0.12;
max_lateral_rel_dist= 0.7;
max_longitudinal_rel_dist = 1.0;
if rel_dist <= avoid_dist
flag = 1;
end
if longitudinal_rel_dist >= max_longitudinal_rel_dist
flag = 1;
end
if abs(lateral_rel_dist) >= max_lateral_rel_dist
flag = 1;
end
end
如图3-25所示,我们在Simulink仿真环境中创建了领头车、跟随车、信号处理模块。其中,领头车的信号处理模块主要负责其运动控制,即绕四个航路点循环往复运动;跟随车的信号处理模块主要负责为强化学习算法提供输入,如状态值、奖励值和仿真结束条件等。
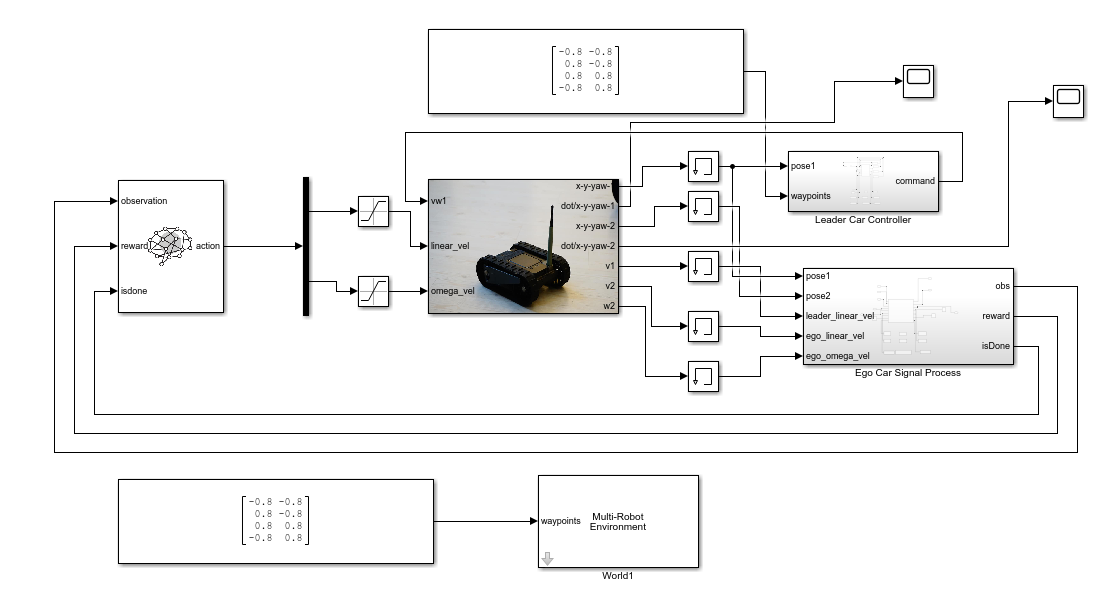
图3-25 基于Simulink的路径跟随环境
四、跟车控制器训练与部署
在Matlab软件的Reinforcement Learning Toolbox™中, 提供了DQN、PPO、SAC 、DDPG和TD3 等经典的强化学习算法,结合这些算法进行策略训练,可以为复杂应用(如资源分配、机器人和自主系统)实现控制器和决策算法。其中,TD3算法是解决连续动作空间的一类强化学习算法,在路径跟随问题中,车辆的控制量(线速度和角速度)也是连续值,符合TD3算法应用的条件。
4.1 TD3训练算法
TD3算法被称为双重延迟深度确定性策略梯度(Twin Delayed Deep Deterministic Policy Gradient,TD3),它是在深度确定性策略梯度(DDPG)算法发展而来的。
4.1.1 网络结构
如图4-1所示,TD3算法的网络结构有6个。其中,Actor网络输入是状态,输出是动作。Critic网络输入是状态和动作,输出是对应的$Q$值。Actor网络的目的是根据状态 $s_t$ ,能够输出使得$Q(s_t,a_t)$最大的动作$a_t$,这个$a_t$越能使$Q(s_t,a_t)$大,就说明网络训练地越好。Critic网络的目的是根据状态动作对$(s_t,a_t)$能够输出其动作值$Q(s_t,a_t)$ ,这个$Q$值越精确,就说明网络训练地越好。
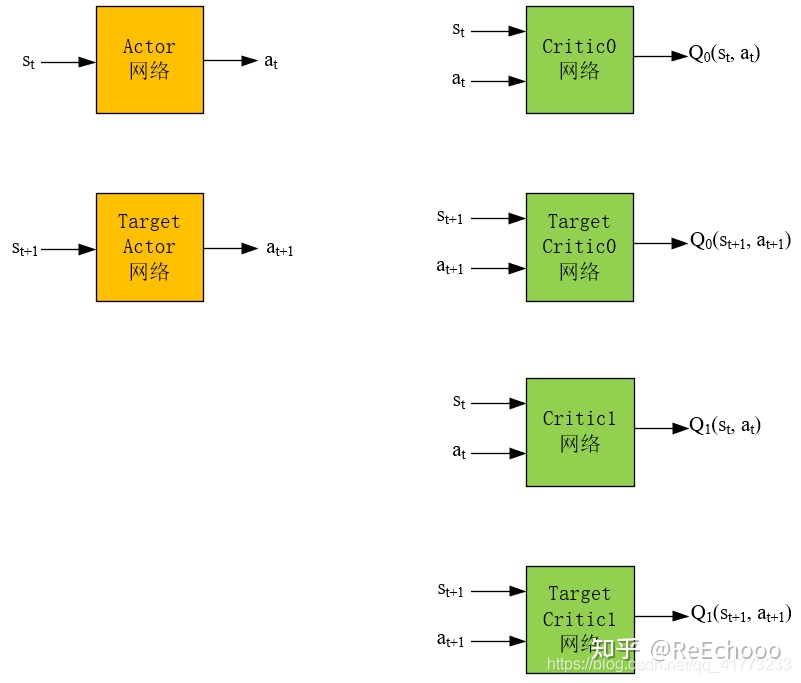
图4-1 TD3算法的网络结构
Actor网络和Target Actor网络的区别是,Actor网络是每步都会在经验池中更新,而Target Actor网络是隔一段时间将Actor的网络参数拷贝到Target Actor网络中,实现Target Actor网络的更新。这种“滞后”更新是为了保证在训练Actor网络时训练的稳定性。同样,Critic网络和Target Critic网络也是为了保证在训练Actor网络时训练的稳定性。
4.1.2 产生经验数据的过程
已知一个状态$s_0$,通过 actor网络得到动作$a'_0$ ,然后再加噪声$N$得到动作$a_0=a'_0+N$ (噪声是为了保证一定的探索,普通的高斯噪声即可),然后将$a_0$输入到环境中,得到$s_1$和$r_1$,这样就得到一个经验数据$(s_0,a_0,s_1,r_1)$ ,然后将经验数据放入经验池中。
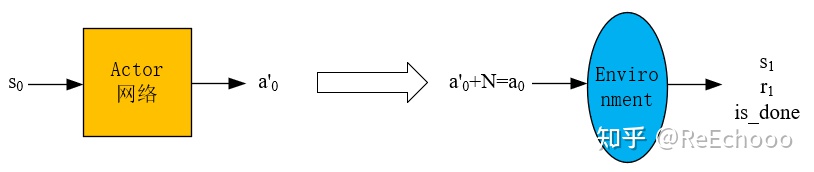
图4-2 Actor网络产生经验数据的过程
经验池 存在的意义是为了消除经验数据的相关性,因为强化学习中前后动作通常是强相关的,将其打散放入经验池中,在训练神经网络时,随机地从经验池中选出一批经验数据,这样能够使神经网络训练地更好。
4.1.3 Actor网络的更新过程
如图4-3所示,Actor网络的损失函数就是$-Q$,$-Q$越小越好,这个$-Q$则由Critic0网络得到。以经验数据$(s_0,a_0,s_1,r_1)$ 为例,将$s_0$输入到Actor网络中,得到预测的动作$a_{0_predict}$,直接将$s_0$和$a_{0_predict}$输入到Critic0网络中,得到$Q$值,然后将$-Q$作为损失函数,修正Actor网络。

图4-3 Actor网络的更新过程
值得注意的是,Actor网络是最重要的,因为它直接决定了智能体采取策略的好坏。想要训练出一个好的Actor网络,需要一个准确的Critic网络来评价它,因此 TD3的剩下5个网络 都是 为了创造 出一个 尽可能精确的Critic网络。
4.1.4 Critic网络的更新过程
Target Actor网络的目的是为了让Critic网络更容易稳定收敛,如果用频繁更新的Actor网络做下一步动作的预测,会导致Critic网络很难收敛, Target Critic网络的目的 与Target Actor网络的目的相同,也是想用一个更新不频繁的网络让Critic网络稳定收敛。
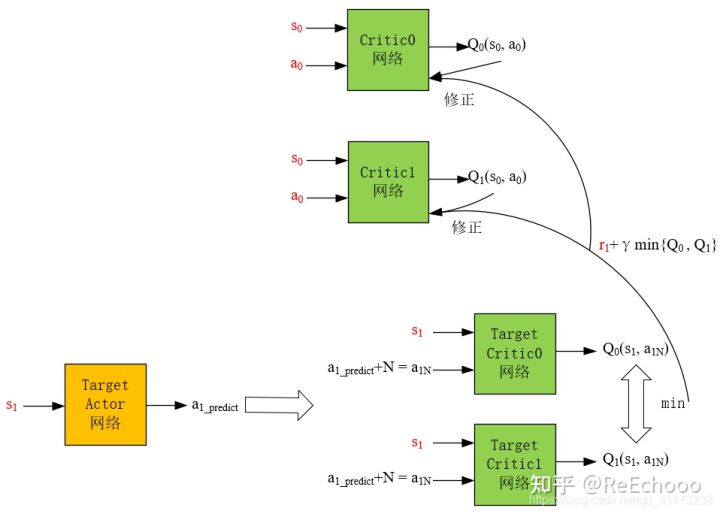
图4-4 Critic网络的更新过程
考虑到在实际的应用中,Critic网络总是过高的估计$Q$值,TD3算法采用两个网络对Q值进行估计,然后选择较小的那个,这样尽可能地 避免过高地估计$Q$值。为此,频繁更新的Critic网络也需要采用两个,用$r_{1}+\gamma * \min \left{Q_{0}\left(s_{1}, a_{1 N}\right), Q_{1}\left(s_{1}, a_{1 N}\right)\right}$来更新两个Critic网络,即用$r_{1}+\gamma * \min \left{Q_{0}\left(s_{1}, a_{1 N}\right), Q_{1}\left(s_{1}, a_{1 N}\right)\right}$分别与$Q_0(s_0,a_0)$和$Q_1(s_0,a_0)$做均方差,然后作为损失值对Critic网络进行梯度下降。
此外,为了鼓励智能体探索, 给Target Actor网络的预测动作**$a_{1_predict}$ **加了一个噪声$N$ ,变为动作$a_{1N}$ 之后,才作为两个Target Critic网络的输入,使得下一步的$Q$值更精确。
4.1.5 TD3算法的优点
一是 将一个Target Critic网络变为两个Target Critic网络,取两者较小的作为下一状态的Q值,从而避免Q值过高地被估计。
二是 对Target Actor 网络的输出进行了加噪声处理,从而使得Target Critic网络的预测输出Q值尽可能精确。
三是 采用了延迟软更新的方式去更新一个Target Actor 网络、两个Target Critic网络,以及采用延迟更新的方式更新Actor网络。
4.2 创建智能体
根据4.1节TD3算法的网络结构,在matlab脚本文件中创建相关的智能体,示例代码如下:
function agent = createPFCAgent(obsInfo,actInfo)
% obsInfo 状态空间信息
% actInfor 动作空间信息
% 获取状态空间和动作空间的维数
numObs = obsInfo.Dimension(1);
numAct = 2;
% 定义Critic网络
statePath1 = [
featureInputLayer(numObs,'Normalization','none','Name','observation')
fullyConnectedLayer(400,'Name','CriticStateFC1')
reluLayer('Name','CriticStateRelu1')
fullyConnectedLayer(300,'Name','CriticStateFC2')
];
actionPath1 = [
featureInputLayer(numAct,'Normalization','none','Name','action')
fullyConnectedLayer(300,'Name','CriticActionFC1')
];
commonPath1 = [
additionLayer(2,'Name','add')
reluLayer('Name','CriticCommonRelu1')
fullyConnectedLayer(1,'Name','CriticOutput')
];
criticNet = layerGraph(statePath1);
criticNet = addLayers(criticNet,actionPath1);
criticNet = addLayers(criticNet,commonPath1);
criticNet = connectLayers(criticNet,'CriticStateFC2','add/in1');
criticNet = connectLayers(criticNet,'CriticActionFC1','add/in2');
criticOptions = rlRepresentationOptions('Optimizer','adam','LearnRate',1e-3,...
'GradientThreshold',1,'L2RegularizationFactor',2e-4);
critic1 = rlQValueRepresentation(criticNet,obsInfo,actInfo,...
'Observation',{'observation'},'Action',{'action'},criticOptions);
critic2 = rlQValueRepresentation(criticNet,obsInfo,actInfo,...
'Observation',{'observation'},'Action',{'action'},criticOptions);
% 定义Actor网络
actorNet = [
featureInputLayer(numObs,'Normalization','none','Name','observation')
fullyConnectedLayer(400,'Name','ActorFC1')
reluLayer('Name','ActorRelu1')
fullyConnectedLayer(300,'Name','ActorFC2')
reluLayer('Name','ActorRelu2')
fullyConnectedLayer(numAct,'Name','ActorFC3')
tanhLayer('Name','ActorTanh1')
];
actorOptions = rlRepresentationOptions('Optimizer','adam','LearnRate',1e-3,...
'GradientThreshold',1,'L2RegularizationFactor',1e-5);
actor = rlDeterministicActorRepresentation(actorNet,obsInfo,actInfo,...
'Observation',{'observation'},'Action',{'ActorTanh1'},actorOptions);
% 设置TD3算法参数
agentOptions = rlTD3AgentOptions;
agentOptions.DiscountFactor = 0.99;
agentOptions.TargetSmoothFactor = 5e-3;
agentOptions.TargetPolicySmoothModel.Variance = 0.2;
agentOptions.TargetPolicySmoothModel.LowerLimit = -0.5;
agentOptions.TargetPolicySmoothModel.UpperLimit = 0.5;
% 创建内置TD3算法的智能体
agent = rlTD3Agent(actor,[critic1 critic2],agentOptions);
end
如图4-5所示,智能体定义完成后,在Simulink主菜单点击“库浏览器”按钮,在弹出窗口搜索栏输入“reinforcement learning”,找到"RL Agent"模块,通过鼠标将其拖入到Simulink的路径跟随环境中,双击"RL Agent"模块,在XXX文本框中填入智能体的名称,例如"agent"。

图4-5 RL Agent设置窗口
4.3 训练智能体
智能体创建完成,需要对智能体的训练环境进行配置,如随机种子、环境重置参数初始化、采样速率、仿真结束时间、最大训练回合数、单个回合的最大步长等。具体示例代码如下:
% 打开Simulink环境
mdl = "m2carRL";
open_system(mdl);
% 设置状态空间和动作空间信息
obsInfo = rlNumericSpec([9 1]);
actInfo = rlNumericSpec([2 1],'LowerLimit',[0.1; 1.0],'UpperLimit',[0.5; 1.0]);
% 创建内置强化学习算法的Simulink环境
blks = mdl + ["/RL Agent"];
env = rlSimulinkEnv(mdl,blks,obsInfo,actInfo);
% 设置环境重置时的初始化函数
env.ResetFcn = @onecarpfcResetFcn;
% 固定随机种子
rng(0);
% 创建智能体
agent = createPFCAgent(obsInfo,actInfo);
% 设置采样速率、仿真时间、最大回合数、单个回合最大步长数
Ts = 0.1;
Tf = 120;
maxepisodes = 30000;
maxsteps = ceil(Tf/Ts);
% 设置训练参数, 如并行训练模式、并行采集线程数、采集数据间隔等
trainingOpts = rlTrainingOptions(...
'MaxEpisodes',maxepisodes,...
'MaxStepsPerEpisode',maxsteps,...
'Verbose',false,...
'Plots','training-progress',...
'ScoreAveragingWindowLength',10);
trainingOpts.UseParallel = true;
trainingOpts.ParallelizationOptions.Mode = "async";
trainingOpts.ParallelizationOptions.DataToSendFromWorkers = "Experiences";
trainingOpts.ParallelizationOptions.StepsUntilDataIsSent = 32;
doTraining = true;
if doTraining
trainingStats = train(agent,env,trainingOpts);
else
load('one_car_pfc__td3_parallel.mat','agent');
end
% 保存训练结果
save('one_car_pfc__td3_parallel.mat', 'agent');
训练智能体的脚本文件编写完成后,点击脚本文件的菜单项“运行”按钮,即可开始训练智能体。如图4-6所示,训练过程中,matlab会自动启动情节管理器,在情节管理器窗口可以查看智能体的训练过程,如当前回合的奖励、近10个回合的平均奖励等。
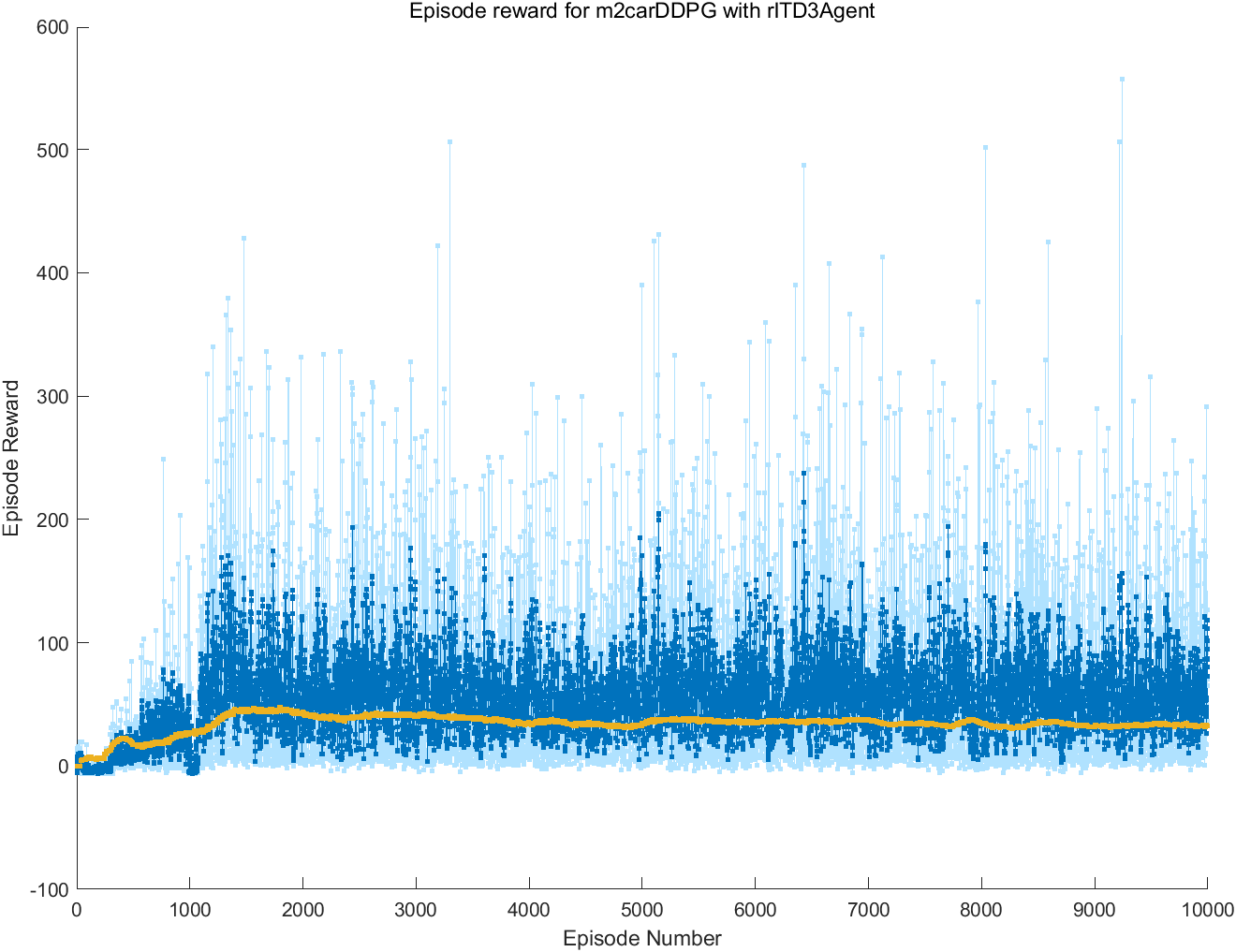
图4-6 情节管理器窗口
训练完成后,可对训练好的智能体进行效果检验,验证的示例代码如下:
% 加载智能体
load('one_car_pfc__td3_parallel.mat','agent');
% 创建验证的Simulink仿真环境
simOptions = rlSimulationOptions('MaxSteps',1200);
experience = sim(env,agent,simOptions);
totalReward = sum(experience.Reward)
4.4 部署智能体
将训练好的智能体部署到实际的虚拟环境或真实环境中,还需要利用matlab的代码生成器生成通用C++代码,供各类系统调用。具体示例代码如下:
load('one_car_pfc__td3_parallel.mat','agent');
generatePolicyFunction(agent, 'FunctionName', "PFC_Policy",'MATFileName',"PFC_Agent.mat");
如图4-7所示,matlab会自动生成PFC_Policy.m和PFC_Agent.mat两个文件,打开PFC_Policy.m文件,其代码内容如下:
function action1 = PFC_Policy(observation1)
%#codegen
% Reinforcement Learning Toolbox
% Generated on: 08-Mar-2022 21:07:29
action1 = localEvaluate(observation1);
end
%% Local Functions
function action1 = localEvaluate(observation1)
persistent policy
if isempty(policy)
policy = coder.loadDeepLearningNetwork('PFC_Agent.mat','policy');
end
observation1 = observation1(:)';
action1 = predict(policy, observation1);
end
图4-7 matlab自动生成的策略文件
可以按照正常脚本文件中的m函数调用即可
4.4.1 基于ROS的虚拟跟车环境
基于第3节所建立的Simulink跟车环境,可以建立类似的基于ROS虚拟跟车环境,利用ROS提供的发布/订阅通信机制实现车辆的控制。如图4-8所示,将matlab自动生成的策略脚本文件封装成控制器模块,供虚拟跟车环境使用,示例代码如下:
function action = one_car_pfc(obs)
action = PFC_Policy(obs);
action = double(action);
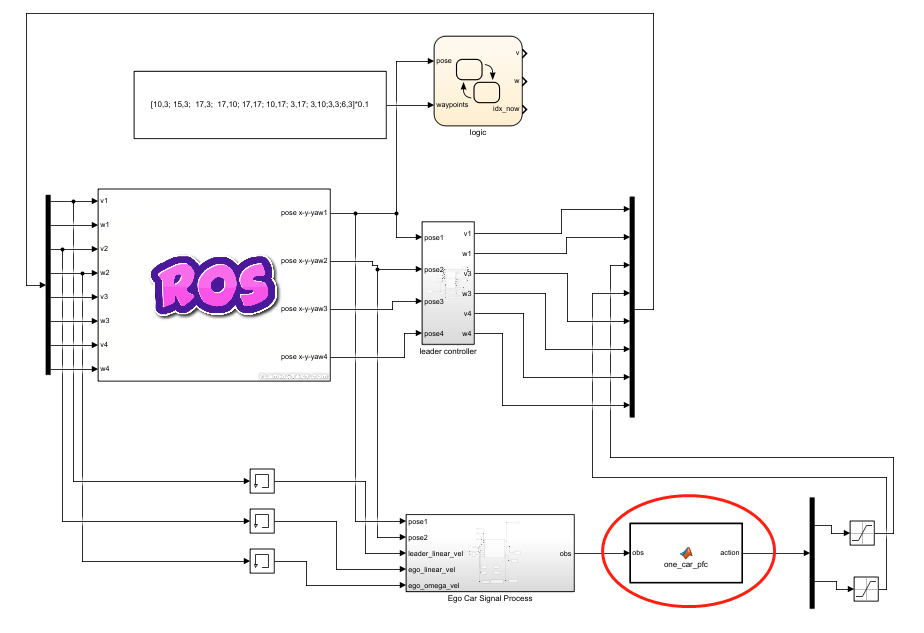
图4-8 基于ROS的路径跟随环境
若需要实现多车跟车效果,相邻的两辆车以前面为领头车、后面为跟随车。例如,环境中有4辆车时,2号车跟随1号车,3号车跟随2号车,4号车跟随3号车,依次类推。如图4-9所示,我们构建了基于ROS的4车路径跟随环境。
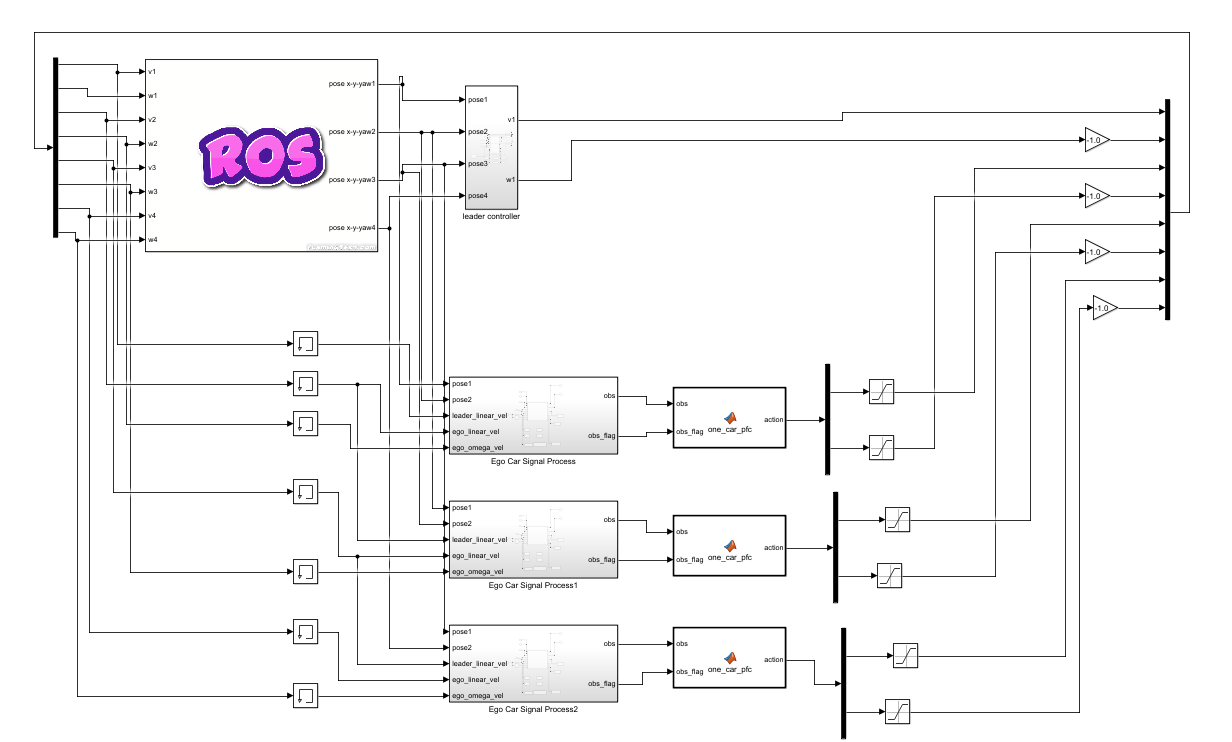
图4-9 基于ROS的多车路径跟随环境
4.4.2 基于ROS的真实跟车环境
若基于ROS的虚拟跟车环境完成后,即可使用真车测试跟车效果。matlab提供了sim2real的实现机制,可将Simulink的代码自动生成支持ROS的执行代码,具体操作步骤是:XXX
五、填坑指南
1. 神经网络输出变量的类型转换问题
matlab编译生成的神经网络模型,其输出类型是single,需要转换成doule类型,否则会报“This assignment writes a 'single' value into a 'double' type. Code generation does not support changing types through assignment. Check preceding assignments or input type specifications for type mismatches.”错误。解决办法详见4.4.1节代码第3行。